Abstract and Introduction:
The work presented here establishes that only a room very closely resembling the one in Figure 2 is completely consistent with (1) the painting itself, Johannes Vermeer’s Officer and Laughing Girl, and (2) what we know, which is substantial, of the sizes and shapes of the things it depicts. An earlier reconstruction by Swillens (1950) is critically evaluated.

Figure 1. Johannes Vermeer, Officer and Laughing Girl, c. 1658, Frick Collection, New York. Scan courtesy of MyStudios.com.

The reconstruction addresses many issues. Among them is this painting’s compactness of scene (Slatkes, 1981, pp. 27-28), considered as an advance in Vermeer’s technique. It is generally conceded that Vermeer’s vantage point was very close to his subjects; the reconstruction shows just how close that was. There is also the matter of whether the room in this painting is, as Swillens (1950) claims, the same room shown in Girl Reading a Letter at an Open Window and The Milkmaid, which he labels “Room D”. Vermeer probably painted all three works between 1657 and 1660 (Schneider, 2000, pp. 94-95), and what may be their common setting does not seem to reappear in the artist’s later works. This suggests Room D was in Mechelen, the family’s inn where Vermeer lived during the early years of his marriage (Steadman, 2001, pp. 60-61; Swillens, pp. 23-24). But we cannot yet be sure that the room in all three paintings has the same size and proportions, which is crucial to the argument.

Steadman (2001, p. 80) points out that Officer and Laughing Girl does not lend itself to the usual reconstructive technique for locating the station point (SP) from which the picture ostensibly is being viewed. Without locating the SP, we cannot reconstruct the 3-D geometry of the original scene. Traditionally, from a grid of ground-plane squares, or at least one such square, visible in the picture, we construct principal distance points (PDPs), which are the vanishing points of diagonals across the grid (Greene, 1983; Sedgwick, 1980; 1991; Steadman, 2001). The PDPs are related in a known way to the SP’s location. But Officer and Laughing Girl does not exhibit a suitable ground plane; an alternative solution is needed. (Technically, the circular rim of the wine goblet in front of the young woman infers a grid square [Greene], and from this we can find the SP. The rim is much too small a feature, though, to assure an accurate result. On the other hand, the casement’s proportion of height to width would have been an excellent basis for a ground-plane-grid, had that been known.)

Apparatus and general procedure:
I took measurements of coordinate points in the painting, from a polychrome reproduction of it that was 37% of the lineal size of the original. Layouts of virtual space were made at one-tenth scale, using a computerized drafting program, MacDraw Pro, Version 1.5v1 (Apple Corporation). Picture-plane coordinates were scaled up and applied to the layouts at the location of the far wall, thereby increasing their accuracy of placement about six-fold. Steadman (2001) and Swillens (1950), in their reconstructive work mentioned, also used reduced-size reproductions for scaling.

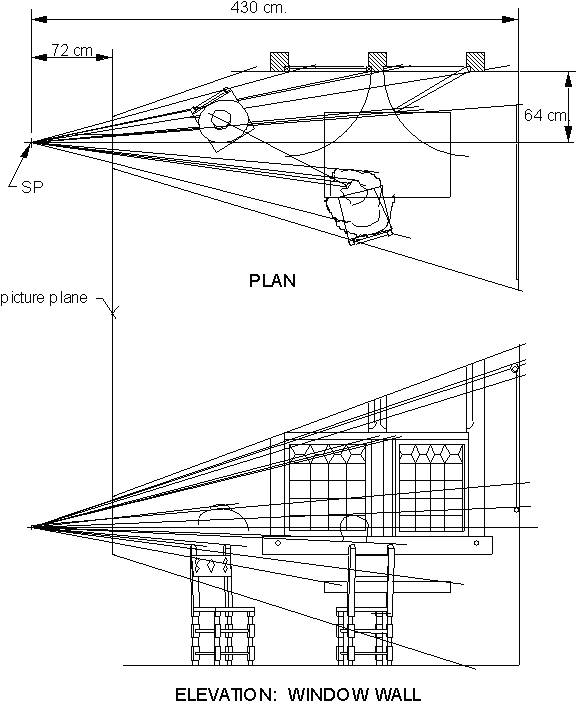
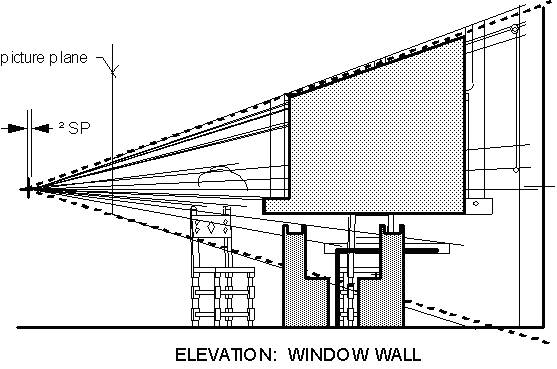
Finding the station point: A set of techniques (Halloran, unpublished), developed from a procedure I had used previously (Halloran, 1989), determined the SP for the reconstruction (Figure 2). This sightline approach is complementary to “Alberti’s veil”, a traditional way of producing the perspective picture by sighting through a transparent surface erected in the picture plane, to determine the positions in the picture of objects in the scene (Alberti, 1991/1435, pp. 65-67). (The two methods for finding the SP, sightline and ground-plane-grid, are ways of working backward through each of the two alternative methods of perspective drawing which Alberti recommended.) To apply the sightline approach, the three requirements are that (1) the picture is a faithfully rendered perspective, (2) we can determine where the line of sight (LOS), which is a perpendicular from the SP, enters the picture surface, and (3) at least one relation is known, between two spatial extents, one in depth and one laterally, that are depicted. (Depth-to-lateral ratios will be wrong in virtual space when the SP distance is wrong.)

Officer and Laughing Girl is a one-point perspective (Greene, 1983; Steadman, 2001) of a rectilinear room, which means, among other things, that the far wall is parallel with the picture surface. Of more immediate interest in finding the SP, the horizontal parallels along the side wall recede directly in depth, parallel with the LOS, in the virtual space being reconstructed. (Virtual space extends from the SP through the picture surface into the entire scene represented.) In the picture, these parallels extending in depth, notably the horizontal edges of the window head and sill, converge toward a single principal vanishing point (PVP). Since the PVP is also the entry point of the LOS, and since the picture seems to be a well-executed perspective, we can locate the SP if we can identify in the picture some measure of depth versus laterality.

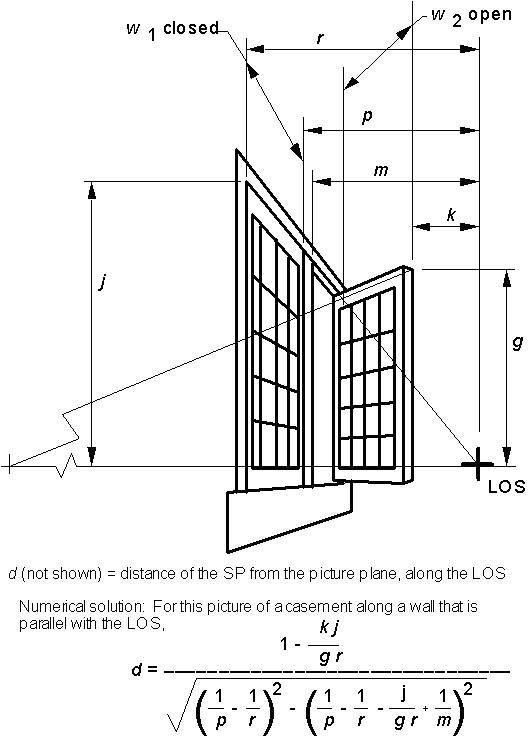
Various features of the scene were examined as potential sources of depth versus lateral information, and discarded. For example, Steadman (n. d.) provides dimensions of a probable exemplar of the officer’s chair. But its angular orientation with the walls, which determines its depth-to-lateral relation, would depend on the SP’s distance, which is what we do not know. The relation I did select is essentially this: The width of the partly opened casement sash must be the same as that of its empty framed opening. The opening extends along the side wall, purely in depth, while the open sash itself extends a distance into the room, and therefore has a lateral component to its width. Changes in SP distance affect the size of extents in depth but not of lateral ones. So, when the SP-to-picture distance is wrong, this will affect the opening and the sash differentially, in virtual space; the framed opening will have suffered a greater increase or decrease in its width than the open sash itself will, making the two no longer the same width.

(Top) Figure 2: Layout of the room in Vermeer’s Officer and Laughing Girl (Halloran, unpublished).
(Bottom) Figure 3: Plan of the room in Vermeer’s Officer and Laughing Girl, in conformance with the way the hinged edge of the open sash is mislocated in the picture.

Unfortunately for the simplicity of the procedural concept just described, there is an anomaly of perspective--the only substantial one I have found in this picture--which had to be considered. The hinge line of the open sash seems to have been displaced leftward on the picture surface, relative to picture-surface coordinates which would match its location in space, assuming (1) that the two sashes really were equal in width, (2) that the real window-framing timbers were all the same size, and (3) that, as the drafted layouts of the room consistently indicate, the rest of the pictured scene is rendered accurately. In other words, the two sashes, as painted, are represented as being of unequal widths, and the far jamb timber of the window is shown as being about twice as wide along the wall as the other windowframe timbers (Figure 3). (The other timbers agree in size with dimensions given by Steadman [2001, p. 98] for the window framing shown in other Vermeer paintings.) To avoid using this displaced hinge line, even if Vermeer shifted it on purpose, as the basis for locating the SP, two complementary departures were made, from the simplest approach: (1) The width of the nearer, closed casement sash, rather than that of the empty opening of the far sash, was designated as the basis for determining each sash-opening’s width. (2) Only the picture-plane coordinates of the near edge of the far sash and of its opening, not the coordinates their common far edge (which is the edge in error), were used in determining the SP. These substitutions, in effect, relocate the the far sash’s hinge line, in virtual space, to the greater depth that would make the two casements the same width and would shrink the farthest window timber to the size of the others, as in Figure 2.

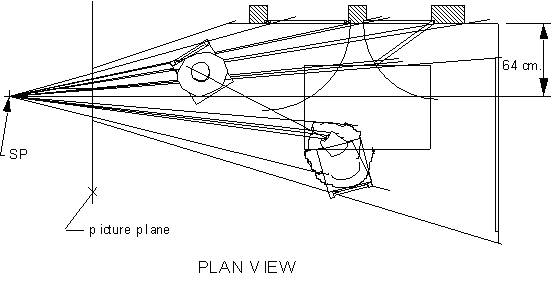
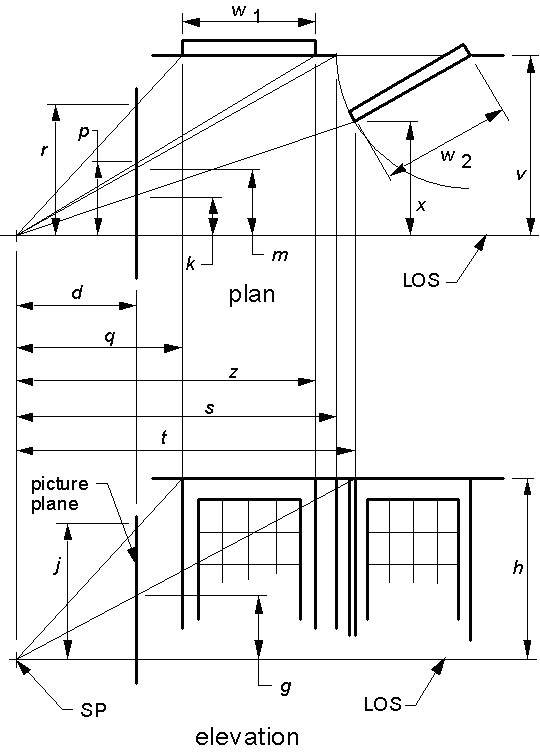
Graphic (Figure 2) and computational (Figures 4 and 5) versions of the sightline approach complemented and verified each other, in establishing the SP distance d. Selecting trial values of d, I drafted iterative plan-and-elevation layouts of the virtual spaces which each trial d produced. The layouts all resemble Figure 2 except in the critical respect of depth-to-lateral proportion. They each verify whether the top near corner of the far sash, and of its opening, as these appear in drawings of the virtual space produced by a particular value of d, fully correspond with the array projections through their depictions, in both plan and elevation views, that is, throughout 3-D virtual space. The range through which this correspondence occurs is the range of acceptable values of d, within which the sash and its empty opening are not detectably different in width. (In making layouts, results from partial-solution equations were used, to establish trial values of d at appropriate intervals of window width.) I also developed, and solved for d, an equation based on the same relation used in the layouts, stated in terms of d and dimensions between picture-plane coordinates (Figure 4). The value for d given in Figure 2 is the result obtained from the equation in Figure 4, and is near the midpoint of the range for d, approximately 64 to 84 cm., indicated by layouts drafted at 16.2-cm. increments of window-embrasure width. These increments are of the length Steadman (2001, p. 98) suggests for mortared bricks of the period.

There was an additional complication in developing a calculational solution for d, that the equation in Figure 4 and the views in Figure 5 do not reflect: The near edge of the closed sash is not very clearly visible, at least in reproductions of the painting. By using enlargements and comparing several reproductions, I was able to determine this edge to my satisfaction. However, I place more confidence in a different set of equations, simultaneously solved for d, which were based on picture-plane coordinates for a vertical line where the inner edge of the closed sash frame meets the glass panes nearest to us, rather than depending on the less certain outer edge of the entire sash. In these equations, it was necessary to add in the width of the wooden sash frame itself, which, because we can measure the window height (see below), can be determined either from this picture or, more easily as it happens, from another painting which seems to show the same window, Girl Reading a Letter at an Open Window. (It proved much easier to solve these equations as a set than to reduce them to a single equation.) The equation in Figure 4, and the set of equations just referred to, yielded identical values for d, of 72 cm.

(Top) Figure 4. Casement dimensions used to develop an equation for the SP distance d, and the equation.
(Bottom) Figure 5. Layout used to develop the equation in Figure 4. (Not to scale.)

Completing the reconstruction:
Beyond finding the SP, if we are to reconstruct the scene itself, we must be able to infer the spatial relations being depicted; moreover, we need the actual size of at least one depicted thing, to know the scale of the reconstruction.

Since the far wall is parallel with the picture surface, that whole wall and things that are flat against it, including intersections with other surfaces, are depicted in their correct shape and proportion, all at the same scale. If the size of even one of its features is known, the whole wall may be scaled directly. Welu (1975, p. 530, Footnote 12) gives dimensions for the map on that wall. Using the horizontal map-only dimension he gives, 154 cm., I scaled the wall’s features, including the height of the window and of the sash it contains, which I was able to do because the horizontals of the head and sill, as extended to the PVP, intersect the back corner of the room. The PVP itself lies along the horizon, which in this case tells us that Vermeer’s eye or his camera was at the same height above the floor as the young woman’s eyes. The PVP is one-third of the horizontal distance from a point directly below the officer’s right eye to the woman’s right eye.

Steadman (2001, p. 78), describes the projective method for placing depicted objects where they belong in virtual space, much as it was used here. The objects were located where their correct size, when that was known, agreed with their optic-array projections, or at the position where some other spatial criterion was met, such as intersection of the array line with a wall. Some features were difficult to locate. It was critical, for example, to determine exactly where the far corner of the room appeared in the picture, because only at that corner could window height be scaled with respect to the map on the back wall. But probably, that corner was coved, and in any case Vermeer rendered it very softly, as a change in hue and shading from which a line of intersection of the walls had to be be interpreted. (Despite this, estimates of where the two wall planes intersect, as measured on two good polychrome reproductions, represented a sash-height variation of less than 1%.) The true size of the table is unknown; the size shown for it in Figure 2 seems to agree with the woman’s sitting height, with her pose and depicted position at the table, and with the location of her chair. It fully matches the projections of the optic array. But there are other table sizes, at least somewhat different, that would do as well.

From chair dimensions given by Steadman (n. d.), the chairs and the floor itself were located thus: First, the officer’s chair-back finials, the lion heads, were projected along array lines into virtual space to the positions where they both have the same elevation, which presumably was the way Vermeer saw them. The young woman’s chair was similarly projected to where its elevation equals that of the man’s chair. (The chair positions were additionally verified by calculation from the picture-surface measurements.) This placement of the chairs, in turn, specified the floor’s elevation. But the chair projections are at such a shallow angle with the horizontal that any slight mismeasure of mine along the way, or of Vermeer’s, for that matter, or any unevenness in the original chairs or floor, would be greatly magnified as a mislocation of the chairs in virtual depth. Considering how delicate these measurements are, it is reassuring to find that the woman has appeared in virtual space at just the place where she ought to appear, in order to receive the strong light from the open sash that in the painting she does receive.

The human figures provide some validation of the furniture placement: The young woman, when seated at the distance dictated by the placement of her chair, would have been someone of just about the average height that Steadman (2001, p. 96) found for the females in the Vermeer paintings he reconstructed. Her sitting height and even her interpupillary distance, which is a fairly stable anthropometric value, are consistent with those of a female this same size, as interpolated from anthropometric tables (U.S. Dept. of Defense, 1991). The placement of the officer’s chair also accords well with his size in depiction, as will be discussed.

What We Learn from the Reconstruction:
Importantly, we learn by reconstructing its virtual space that Officer and Laughing Girl, fundamentally and in most of its details, is made in correct perspective, but that a single, significant departure from that correctness exists: Welu (1975, p.531) considers “the dramatic foreshortening of the window to the left” in this painting, as evidence that Vermeer used a camera obscura. Welu does not claim that this foreshortening involves any mistake in perspective, but a comparison of Figure 2 with Figure 3 shows just such an error in the picture; effectively, the window is foreshortened more than, in correct perspective, it would be. Since, in shifting the hinge line, Vermeer has made the sash look more widely open, he may have done it for that purpose. Otherwise, it is a type of error that Hockney (2001) attributes to the use of optical projecting devices of an unstable kind, which tend to shift position as an artist works, although the particular device he considers most likely to cause this problem, the camera lucida, probably was not available to Vermeer. Welu seems to argue that, without the close working and viewing distances the camera obscura afforded, Vermeer might not have gotten the same degree of foreshortening in this painting. In Figure 2, the distance from the SP to the nearest object in the scene, which is the back of the officer’s chair (or perhaps his elbow), is about 1.4 meters, and is almost exactly twice the distance that the picture plane was from Vermeer’s eye, if his aid to drawing (assuming he needed one) was an Alberti’s veil instead of a camera obscura. The latter device would indeed have been helpful, but it seems unlikely that his composition depended on it. (On the other hand, it does seem that Vermeer somehow maintained a single vantage point very exactly, over a period of time.)

We learn the sizes of things in the scene. Based on the measurements and calculations supporting Figure 2, the total width of the window embrasure is approximately 190 cm.; each openable sash is 86 cm. tall by 76 cm wide. The open sash is swung inward about 30° from the window frame, assuming the 76-cm. width for both sash. (However, as depicted with the hinge incorrectly shifted toward our viewpoint, in Figure 3, that sash has swung 35°, and is only 65 cm. wide; the closed sash remains 76 cm. wide.) The floor is approximately 114 cm. below the top of the windowsill, which in turn is 8 cm. below both the LOS and the young woman’s eyes. The room size matches what is known of the overall width of Mechelen (about 7 meters; see Steadman, 2001, pp. 98, 99). The room as laid out in Figure 2 also agrees with an old engraving which shows the inn as having two full-height windows in its facade; see Figure 6. On the assumption that the room extended the full width of the building, Figure 2 suggests there would have been a comfortable amount of working space behind the station point for an artist and artist’s tools, including a camera obscura if Vermeer used one.

Figure 6. Vermeer’s house, Mechelen: Redrawn by the author from Swillens (1950, Plate 35b). Swillens’ Plate 35a is labeled, “The Market at Delft, Engraving by L. Schenk, after a drawing by Abr. Rademaker, [ca.] 1732.” Plate 35b is a detail of that engraving, labeled as “Mechelen”.

We gain in critical insight. Welu (1975, p. 531) discusses the “extreme difference in size between the soldier and the girl” only in terms of Vermeer's having used a camera obscura. But it could be that the man seems so much larger simply because he is sitting at quite a distance forward from the table. (I find the center of his chair seat to be 90 cm. closer to the SP than is the near edge of the table.) The woman is about 1.7 times farther from us than the officer, so that he ought to have almost twice her dimensions in the picture, as he does. In his 3-D reality, he does not seem to have been especially tall: As reconstructed, his erect sitting height is only 2 or 3 cm. greater than hers, allowing for likely differences in clothing thickness and the fact that she is leaning forward. Interpolating from anthropometric tables for modern values of sitting eye height (U.S. Dept. of Defense, 1991), he is roughly a 10th percentile male, she a 25th percentile female. Although such estimates are very error-prone, this suggests that he is about 166 cm. (5’-5”) in standing height; she, 158 cm. (5’-2”).

We may compare the spaces in different pictures: There is just about enough space in the back corner of the room shown in Officer and Laughing Girl, to put a chair where one is placed in Girl Reading a Letter at an Open Window; this reinforces Swillens’ (1950) conviction that both paintings show the same room. We also may compare this reconstruction of Officer and Laughing Girl with the one by Swillens; see Figure 7 and the discussion below.

P. T. A. Swillens’ Reconstruction of Officer and Laughing Girl:
There are strong reasons to doubt the correctness of Swillens’ orthographic drawing (Swillens, 1950, Plate 50b; also reproduced in Steadman, 2001, p. 81, Figure 34a) of this painting: (1) His description of his reconstructive approach (pp. 69-77) is diffuse and sketchy, and what he tells us concerning Room D is not reassuring. He generally used the ground-plane-grid method, which it does not seem will give a direct solution for any of the Room-D paintings. Presumably because it will not, he says (p. 75) he determined the size and proportions of Room D by assuming that its windowpanes (“division of the windows”) were the same size as in Lady Standing at the Virginal (his Plate 49)--which shows a distinctly different room, very likely in a different building, making this a doubtful thing to assume. (2) The drawing of Officer and Laughing Girl is incomplete. His plan view contains only the LOS and the position of the open sash, nothing else. Neither the map, the picture plane, nor either of the human figures appears in either view, although Swillens does make clear that he used maps and furniture as bases for scaling. (3) Several of Swillens’ drawings contain visible errors of varying importance. Windows are incorrectly drafted. For example, in his elevation view of Girl Reading a Letter at an Open Window, the windowsill timber becomes part of the open sash. More seriously, that same drawing indicates a one-point perspective, which cannot be reconciled with the vertical perspective taper in that painting. Also, Steadman (2001, p. 80 and his Figures 34, 35) finds that Swillens has placed the SP for The Love Letter “much nearer to the subject than it really is.”

Figure 7. Two versions of the room in Officer and Laughing Girl. The outlines of an elevation drawing by P. T. A. Swillens (1950, Plate 50b), indicated by thicker lines and shading, are superimposed on the relevant portion of Figure 2, at a common scale.

In Figure 7, I have superimposed Swillens’ (1950) elevation view of Officer and Laughing Girl on my own. His SP distance d is slightly longer than mine. His and my windows are well-centered on each other; they have the same elevation with respect to the LOS, and their casements are equally tall. His window is 20% narrower than mine. Remarkably, since he almost certainly used a very different method, his values of d, window width, and distance from the SP to the back wall are very close to what the sightline approach will give, if Vermeer’s shift of the far hinge line is ignored ((by simply comparing the open sash with its own enclosure). (Using a set of equations developed from this simplified relation, I found d to be 75 cm., sash width w to equal 65 cm., and the distance from the SP to the back wall to be 449 cm.--vs. the approx. 76 cm., 61 cm., and 450 cm., respectively, measured from Swillens’ drawing.)

Swillens shows chair backs which are shorter than their optic projections will allow, but the floor is the same elevation below the LOS in both his and my reconstructions. (He determined the floor elevation [1950, p. 74] in all three Room-D paintings from that in The Milkmaid.) His table and mine are nearly the same height. In his plan view, the LOS is the same distance from the window wall as in mine. However, he places the officer’s chair much farther from the SP than I do, and has the woman’s chair at a different angle with the walls.

In sum, the drawing by Swillens is incomplete and provides only depth and height information for the furniture. Still, it seems accurate, except in two major respects: Swillens assigned too short an overall height to the chairs, which may have seriously affected their placement in the room. Also, his window is too narrow, and the space he shows between the end of the window and the far wall is consequently too large. His floor elevation agrees with mine, although it was arrived at differently.

Concluding comment, as an antidote to so much detail:
In general, we do not see things in pictures as accurately as if the real scene were present before us, because pictures give us only some of the perceptual information a real scene affords. Reconstructions of virtual space can help us bridge the gap, though. At least in our mind’s eye, we can pace off the room shown in a picture or see it from any angle, and we can measure it up with a ruler, for a much better spatial understanding of what the photographer or artist thought was so worth looking at.